Magonty et le nombre d'or
par Serge Degueil
Oui, il s’agit bien du fameux nombre qui enchanta pendant des siècles des générations de bâtisseurs, mathématiciens, philosophes, artistes et poètes. C’est le nombre que les dieux ont créé pour gérer l’harmonie du monde. Les fouilles du temple d'Andros montrent qu’il y a déjà 10 000 ans les hommes avaient conscience de cette harmonie. 2800 av. J.C., la pyramide de Kheops présente des dimensions qui répondent au nombre d'or. Le sculpteur grec Phidias, Ve siècle avant J.C., utilise le nombre d'or pour bâtir le Parthénon à Athènes. Mais quel est ce nombre que l’on appelle F en l’honneur de ce grand sculpteur ? Comme pour le nombre p, c’est un nombre qui possède une infinité de décimales :
F = 1,618 033 988 749 894 848 204 586 834 365 638 117 720 309 179 805 762 862 135 448 622 705 260 462 189 …
Les hommes l’ont rapidement approché car il est partout présent dans la nature. Mais qu’a t-il de si extraordinaire ?
Sans faire de puissantes mathématiques, regardons la liste des chiffres ci-dessous.
0.235 ; 0.382 ; 0.618 ; 1 ; 1.618 ; 2.618 ; 4.236
On constate que 0.235 + 0.382 = 0.618
0.382 + 0.618 = 1
0.618 +1 = 1.618
1 + 1.618 = 2.618
1.618 + 2.618 = 4.236 …
En prenant F= 1.618 comme nombre de base on a :
F2 = 2.618 ; F3 = 4.236...
1/F = 0.618 ; 1/F2 = 0.382 ; 1/F3 = 0.235 ...
Φ est le seul nombre au monde qui permet d’associer une progression arithmétique et une progression géométrique. De ce fait il crée une harmonie à laquelle l’être humain est sensible.
De ce constat, on a F2 = F + 1 et F est la racine positive de l’équation F2 - F - 1= 0
F = (1 + Ö5)/2 =1.618033....
À partir de là, on peut définir :
- la section d’or ou divine proportion (en1498 le moine Fra Luca Pacioli, professeur de mathématiques, écrit De divina proportione).
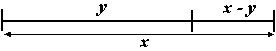
x / y = 1.618 et (x-y) / y = 1.618
- le rectangle d’or
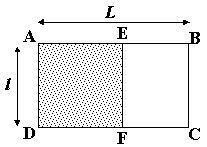
AD / AB = EB / EF = 1.618 dans lequel ADFE est le carré d’or
- les triangles d’or et le pentagone d’or
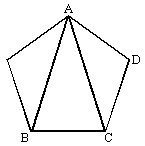
AC / BC = F
AC /AD = F
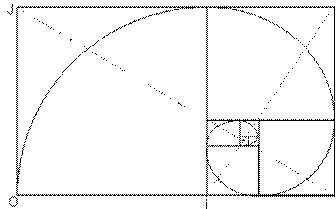
- la spirale d’or
De ces quelques figures de base, on peut élaborer de nombreuses autres figures comme la spirale d’or qui est construite à partir du rectangle d’or.
Les réalisations de la nature.
La nature a su exploiter les propriétés du nombre d’or pour se développer de manière harmonieuse. Voici quelques exemples.
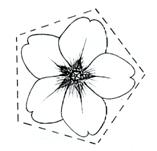
Le nautile respecte parfaitement les paramètres de la spirale d’or, la primevère ainsi que toutes les fleurs pentamères entrent dans le pentagone d’or.


L’homme aussi répond à ces critères car la nature lui a aussi donné tous les outils nécessaires pour réaliser ses œuvres
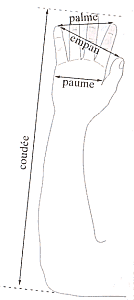
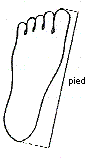
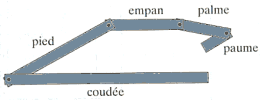
Coudée/pied = pied/empan = empan/palme = palme/paume = 6.18
Coudée = pied + empan
Pied = empan + palme
Empan = palme + paume
Cette caractéristique du nombre d’or a donné naissance à une pige, la canne du bâtisseur et la corde à 12 nœuds qui ont servi de règle, de compas, d’équerre, mais aussi de gabarit pour les angles complexes et différentes figures géométriques dont le pentagone dans lequel l’homme s’inscrit parfaitement. Ces instruments ont permis, pendant des siècles, aux grands maîtres d’oeuvre de réaliser les chefs d’œuvres qui nous fascinent toujours, que ce soit en peinture ou en architecture.
Les abbayes cisterciennes en particulier, qui nous frappent par leur sérénité, sont construites suivant les règles du nombre d’or comme le montre le profil des voûtes en « berceau brisé ».
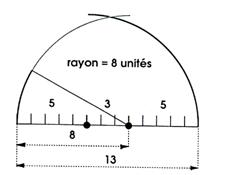
13/8 ≈ 8/5 ≈ 5/3 ≈ Φ
Mais il existe bien d’autres merveilles dans le monde
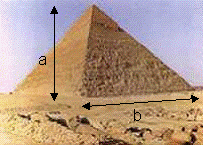
a /(½b) = F

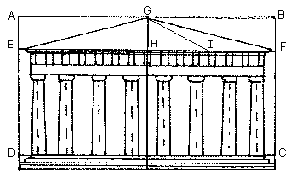
ED/EF =F GI/GF = F
Mais revenons un peu aux mathématiques. Considérons une suite, dans laquelle un nombre est la somme des deux nombres qui le précède comme pour la construction de la progression arithmétique du nombre d’or.
0-1-1-2-3-5-8-13-21-34-55-89-144…
Cette suite de nombre est appelée suite de Fibonacci (Pise 1175). Si on fait le rapport de 2 nombres consécutifs on constate que plus le nombre est grand et plus on se rapproche du nombre d’or. Pour les mathématiciens avertis, on dira que cette suite converge vers le nombre d’or.
3/2 = 1.5 13/8 = 1.625 89/55 = 1.618
Si on revient aux propriétés des deux progressions arithmétiques et géométriques liées à F, on peut écrire :
F2 = F+1
F3 = F2 + F = F + 1 + F = 2F +1
F4 = F3 + F2 = (2F + 1) + (F + 1) = 3F + 2
F5 = F4 + F3 = (3F + 2) + (2F + 1) = 5F + 3
F6 = 8F + 5
F7= 13F + 8
.....
On constate là encore que les puissances du nombre d’or s’expriment en fonction de F et que les coefficients ne sont rien d’autres que les nombres de Fibonacci. Ceci prouve le lien très étroit entre le nombre d’or et la suite de Fibonacci et le rapport entre 2 coefficients successifs tend vers f.
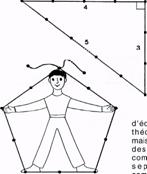
Bien avant le 12e siècle, les Grecs avaient découvert cette propriété comme le prouve la répartition des gradins dans le théâtre d’Epidaure ; 55 gradins au total répartis en 2 séries, l’une de 34 rangées l’autre de 21 rangées. Ces trois nombres, 21, 34 et 55 appartiennent à la suite de Fibonacci et on a :
34 / 21≈ Φ et (34+21)/34= Φ

Et Magonty dans tout ça ?
Vous savez tous que l’emblème de quartier de Magonty est la pomme de pin, la pigne. Vous ne voyez toujours pas?
Prenez une pomme de pin, retournez la et regardez l’implantation des écailles que sa base dessine. Vous constatez qu’elles se développent suivant deux séries de spires tournant en sens contraire. On trouve 8 spires dans un sens et 13 dans l’autre, deux nombres de la suite de Fibonacci dont le rapport est très voisin de Φ.
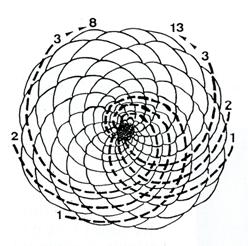
Il en est de même avec les feuilles d’artichaut ou les graines de tournesol.
Mais encore. Regardons notre bonne maison de quartier. C’est pratiquement un pentagone d’or.
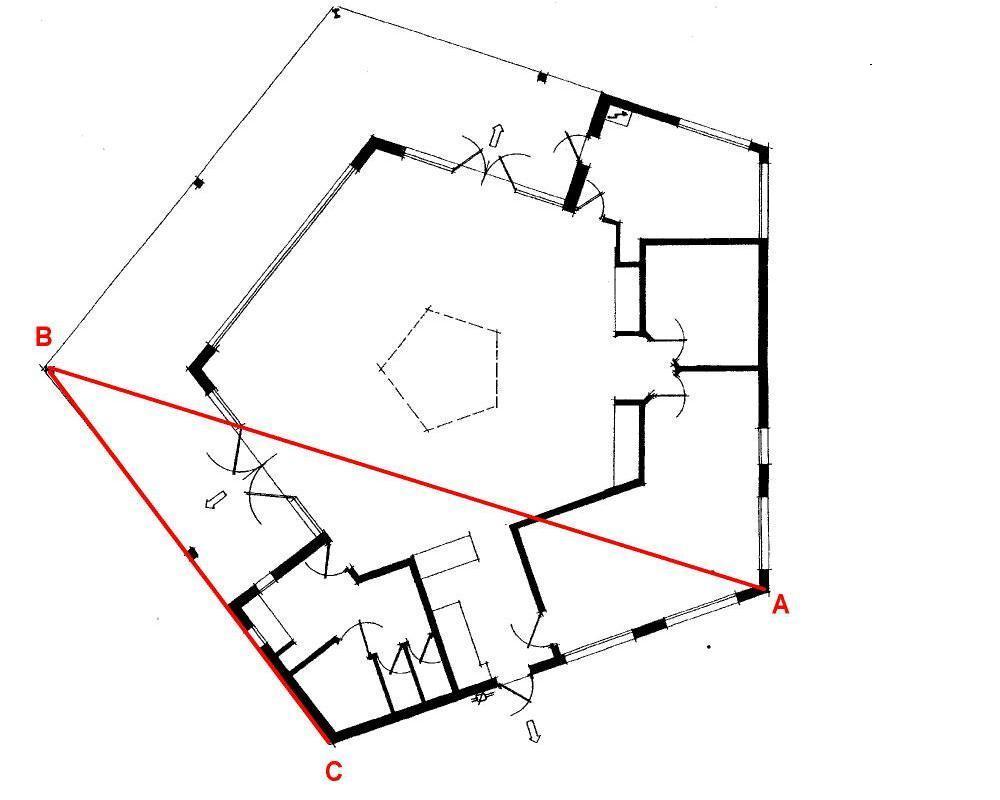

AB/BC = 19,7/12,2= 1.614
Nous voyons donc que nous pouvons être confiants. Magonty se développe de façon harmonieuse en suivant les grands principes universels. Nous veillerons à ce que cela se perpétue et en particulier pour les futurs projets développés sur le quartier, nous nous assurerons qu’ils satisfassent bien au nombre d’or.
Bibliographie :
- Mireille Hartmann, L’enfant et le nombre d’or, Éditions Abbaye de Boscodon
- Marius Cleyet-Michaud, Le nombre d’or, Collection Que sais-je ? Presses Universitaires
- Bâtisseurs au Moyen Âge, Éditions de l’Instant Durable
- Documentation Internet